Ein musikalisches Intervall ist ein Höhenunterschied zweier Töne. Physikalisch stellt dies einen Frequenzunterschied bzw. ein Frequenzverhätnis zwischen diesen beiden Tönen dar. Eine Oktave entspricht einem Frequenzverhältnis von 2, d.h. ein Ton ist genau dann eine Oktave höher, wenn seine Frequenz doppelt so groß ist. Ein Intervall klingt dann konsonant (harmonisch), wenn dessen Frequenzverhältnis exakt oder mit guter Näherung einem Bruch entspricht bei dem in gekürzter Form der Zähler und der Nenner möglichst klein sind. In diesem Falle treffen nämlich die Frequenzen der Oberschwingungen der Musikinstrumente aufeinander.
Soll die Harmonie eines Frequenzverhältnisses n/d linear zum Anteil der Oberschwingungen des ersten Tones, die mit denen des zweiten Tones zusammentreffen, und ebenfalls linear zum Anteil der Oberschwingungen des zweiten Tones, die mit denen des ersten Tones zusammentreffen, sein, dann könnte man ein Maß für die Konsonanz eines Intervalles mit einem solchen Frequenzverhältnis bei Teilerfremden n und d wie folgt definieren:
q(n/d) = 1/(n×d)
Hierbei bliebe jedoch unberücksichtigt, dass z.B. ein Frequenzverhältnis von 151/100 = 1.51 vom Menschen nahezu genauso wie das Frequenzverhältnis 3/2 = 1.5 wahrgenommen wird. Je ungenauer das exakte Verhältnis 3/2 jedoch getroffen wird, desto dissonanter wird das Intervall. Wir müssen also berücksichtigen, dass die Wahrnehmung von Frequenzen und damit auch von Frequenzunterschieden "unscharf" erfolgt. Im Folgenden nehmen wir zur Modellierung dieses Phänomens bei jedem einzelnen Ton eine Unschärfe der Frequenz an, die genau dem Frequenzverhältnis entspricht, welches von einem Menschen bei zwei aufeinander folgenden Tönen gerade noch wahrgenommen werden kann. Auf der logarithmischen Skala sind dies etwa 6 cent, entsprechend einem Verhältnis von 2^(6/1200) = 1.00347.
Möchte man nun die Unschärfe eines Frequenzverhältnisses zweier Töne bestimmen, so ist die Unschärfe der Frequenzen BEIDER Töne zu berücksichtigen. So wie sich jedoch auch nicht die Standardabweichung zweier addierter normalverteilter Zufallsgrößen addiert, sondern sich die Quadrate der Standardabweichungen (die Varianzen) addieren, so addieren wir analog hierzu auch bei der Unschärfe die Quadrate, und erhalten dann √(6 cent)² + (6 cent)² = √2 × 6 cent als Unschärfe von Intervallen.
Berücksichtigen wir diese Unschärfe nun bei der Berechnung eines Maßes für die Konsonanz eines Intervalles, und suchen wir zu jedem reellen Frequenzverhältnis das am besten passende rationale Frequenzverhältnis, so erhalten wir bei Verwendung der Normalverteilung zum Darstellen der Unschärfe die folgende Formel:
Q(x) = maxn,d ∈ ℕ [ exp (−1/2 × (log2(x ÷ n/d) × 1200 cent ÷ (√2 × 6 cent))2) × q(n/d) ]
Q(x) = maxn,d ∈ ℕ [ exp (−10000 × (log2(x ÷ n/d))2) ÷ (n × d) ]
Der Kurvenverlauf der Funktion Q(x) sieht wie folgt aus:
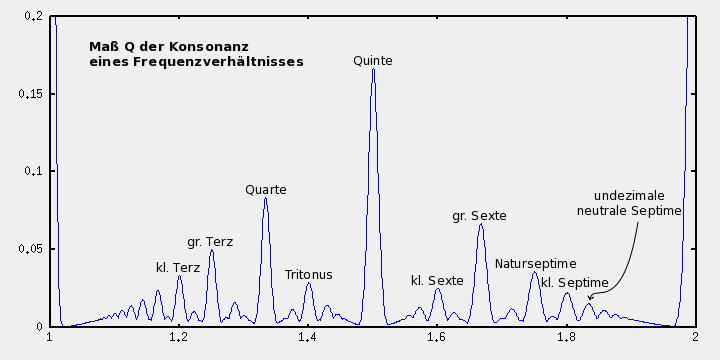
Zwischen der Prime (ganz links) und der Oktave (ganz rechts) finden wir Peaks für die bekannten musikalischen Intervalle, z.B. große und kleine Terz, Quarte, Quinte und weitere. Das Bild ist nicht symmetrisch, auch wenn es auf den ersten Blick so scheint. Es ist zu betonen, dass diese Funktion auf sehr einfachen Modellen basiert, die nicht unbedingt mit der tatsächlich wahrgenommenenen Konsonanz/Dissonanz übereinstimmen müssen. So ist z.B. die Wahrnehmungsschwelle eines Tonhöhenunterschiedes in Wirklichkeit frequenzabhängig und lässt sich auch nicht direkt auf die Toleranz in Bezug auf Harmonien übertragen. Die Annahme das Empfinden von Konsonanz eines Intervalls sei bilinear zum Übereinstimmen der Oberschwingungen beider beteiligter Töne ist ebenfalls lediglich ein Modell und entspricht nicht exakt der Realität. Die Oberschwingungen sind je nach verwendetem Musikinstrument unterschiedlich stark ausgeprägt, was auch Auswirkungen auf das Harmonieempfinden hat, hier jedoch unberücksichtigt bleibt.
Wir betrachten nun Tonsysteme bei denen die Oktave in gleich große Tonschritte eingeteilt wird. Bei n Schritten pro Oktave entspricht ein Tonschritt dann einem Frequenzverältnis der n-ten Wurzel aus 2. Zur Beurteilung der Güte des Harmonievorrates eines solchen Tonsystemes berechnen wir das durchschnittliche Maß der Konsonanz aller sich ergebender Intervalle, die größer als die Prime und kleiner als die Oktave sind. Um zu vermeiden, dass mehrere Intervalle des gleichstufigen Tonsystemes auf Basis ein und des selben zugrundeliegenden rationalen Frequenzverhältnisses bewertet werden, streichen wir den Peak für die Prime (Verhältnis 1/1) und die Oktave (Verhältnis 2/1) aus der Bewertungsfunktion Q und bewerten hiermit zunächst nur das konsonanteste Intervall. Der dem konsonantesten Intervall entsprechende Peak wird dann für die Bewertung der folgenden Intervalle ebenfalls gestrichen. Diese Verfahrensweise wird wiederholt, bis alle Intervalle bewertet wurden, und der Durchschnitt errechnet werden kann. Grafisch stellen sich die Ergebnisse wie folgt dar:
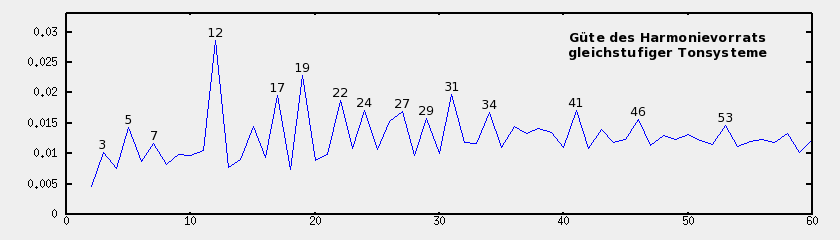
Dem Modell nach haben die geeignetesten gleichstufigen Tonsysteme folgende Anzahlen von Tönen pro Oktave: 12, 19, 31, 17, 22, 24.
Diese möchte ich im Folgenden detailierter betrachten:
Die meiste Musik unseres Kulturkreises verwendet heutzutage dieses Tonsystem von 12 gleichgroßen Tonschritten (entsprechend einem Frequenzverhältnis der zwölften Wurzel aus 2).
| Anzahl (Halb-)Tonschritte |
reelles Frequenzverhältnis |
genähertes rationales Frequenzverhältnis |
Name des Intervalls | Abweichung in Cent |
|---|---|---|---|---|
| 1 | 1.05946 | 18:17 | + 1.0 cent | |
| 2 | 1.12246 | 9:8 | große Sekunde (größere Variante) | − 3.9 cent |
| 3 | 1.18921 | 6:5 | kleine Terz | − 15.6 cent |
| 4 | 1.25992 | 5:4 | große Terz | + 13.7 cent |
| 5 | 1.33484 | 4:3 | reine Quarte | + 2.0 cent |
| 6 | 1.41421 | 17:12 | − 3.0 cent | |
| 7 | 1.49831 | 3:2 | reine Quinte | − 2.0 cent |
| 8 | 1.58740 | 8:5 | kleine Sexte | − 13.7 cent |
| 9 | 1.68179 | 5:3 | große Sexte | + 15.6 cent |
| 10 | 1.78180 | 16:9 | kleine Septime (kleinere Variante) | + 3.9 cent |
| 11 | 1.88775 | 17:9 | − 1.0 cent | |
| 12 | 2.00000 | 2:1 | Oktave | ± 0.0 cent |
Auffallend ist, dass die große und kleine Terz mit 13.7 und 15.6 cent verhältnismäßig stark von den korrekten rationalen Frequenzverhältnissen 5:4 und 6:5 abweichen.
| Anzahl Tonschritte |
reelles Frequenzverhältnis |
genähertes rationales Frequenzverhältnis |
Name des Intervalls | Abweichung in Cent |
|---|---|---|---|---|
| 1 | 1.04162 | 24:23 | − 3.1 cent | |
| 2 | 1.08496 | 13:12 | + 2.6 cent | |
| 3 | 1.13012 | 9:8 | große Sekunde (größere Variante) | + 7.9 cent |
| 4 | 1.17715 | 13:11 | − 6.9 cent | |
| 5 | 1.22613 | 11:9 | undezimale neutrale Terz | + 5.5 cent |
| 6 | 1.27716 | 9:7 | septimale große Terz | − 11.6 cent |
| 7 | 1.33031 | 4:3 | reine Quarte | − 3.9 cent |
| 8 | 1.38567 | 18:13 | + 1.3 cent | |
| 9 | 1.44334 | 13:9 | − 1.3 cent | |
| 10 | 1.50341 | 3:2 | reine Quinte | + 3.9 cent |
| 11 | 1.56597 | 11:7 | undezimale kleine Sexte | − 6.0 cent |
| 12 | 1.63114 | 13:8 | + 6.5 cent | |
| 13 | 1.69902 | 17:10 | − 1.0 cent | |
| 14 | 1.76973 | 16:9 | kleine Septime (kleinere Variante) | − 7.9 cent |
| 15 | 1.84338 | 11:6 | undezimale neutrale Septime (größere Variante) | +9.5 cent |
| 16 | 1.92009 | 23:12 | + 3.1 cent | |
| 17 | 2.00000 | 2:1 | Oktave | ± 0.0 cent |
Musik die sich dieses Tonsystemes bedient wirkt im Vergleich zu den üblicherweise verwendeten Tonsystemen sehr fremdartig, da sich im gleichstufigen Tonsystem mit 17 Tönen je Oktave keine große oder kleine Terz darstellen lässt, jedoch andere ungewöhnlichere Intervalle entstehen, wie z.B. die septimale große Terz mit einem Frequenzverhältnis, welches den Primfaktor 7 enthält, oder die undezimale neutrale Septime mit dem Primfaktor 11 im Frequenzverhältnis.
| Anzahl Tonschritte |
reelles Frequenzverhältnis |
genähertes rationales Frequenzverhältnis |
Name des Intervalls | Abweichung in Cent |
|---|---|---|---|---|
| 1 | 1.03716 | 27:26 | − 2.2 cent | |
| 2 | 1.07569 | 14:13 | − 2.0 cent | |
| 3 | 1.11566 | 10:9 | große Sekunde (kleinere Variante) | + 7.1 cent |
| 4 | 1.15711 | 7:6 | septimale kleine Terz | − 14.2 cent |
| 5 | 1.20010 | 6:5 | kleine Terz | +0.1 cent |
| 6 | 1.24469 | 5:4 | große Terz | − 7.4 cent |
| 7 | 1.29094 | 9:7 | septimale große Terz | + 7.0 cent |
| 8 | 1.33890 | 4:3 | reine Quarte | + 7.2 cent |
| 9 | 1.38865 | 7:5 | Huygens' Tritonus (übermäßige Quarte) | − 14.1 cent |
| 10 | 1.44025 | 13:9 | − 5.0 cent | |
| 11 | 1.49376 | 3:2 | reine Quinte | − 7.2 cent |
| 12 | 1.54926 | 14:9 | septimale kleine Sexte | − 7.0 cent |
| 13 | 1.60682 | 8:5 | kleine Sexte | + 7.3 cent |
| 14 | 1.66652 | 5:3 | große Sexte | − 0.1 cent |
| 15 | 1.72844 | 19:11 | + 1.2 cent | |
| 16 | 1.79266 | 9:5 | kleine Septime (größere Variante) | − 7.1 cent |
| 17 | 1.85927 | 13:7 | + 2.0 cent | |
| 18 | 1.92835 | 27:14 | − 0.2 cent | |
| 19 | 2.00000 | 2:1 | Oktave | ± 0.0 cent |
Man sieht, dass fast alle auch vom 12-stufigen System getroffenen rationalen Frequenzverhältnisse im 19-stufigen Schema enthalten sind: kleine und große Terz, reine Quarte, reine Quinte sowie die kleine und große Sexte. Anstelle der größeren Variante der großen Sekunde (Frequenzverhältnis 9:8) ist hier die kleine Variante mit einem Frequenzverhältnis von 10:9 zu finden. Ebenso ist statt der kleineren Variante der kleinen Septime (Frequenzverhältnis 16:9) die größere Veriante mit dem konsonanteren Frequenzverhältnis von 9:5 enthalten. Quarte und Quinte sind gegenüber dem 12-stufigen System schlechter getroffen, die große und ganz besonders die kleine Terz sind im 19-stufigen System jedoch wesentlich besser abgebildet.
Durch die Ähnlichkeit zum 12-stufigen System lässt sich eine Tastenanordnung schaffen, die der typischen Anordnung auf dem Klavier sehr ähnlich ist. Solche Anordnungen fanden sich laut Wikipedia bereits im 16. Jahrhundert:
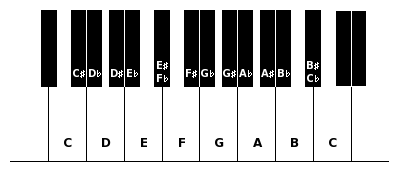
Cis und Des, Dis und Es usw. sind nicht auf ein und derselben Taste zu finden, sondern auf zwei verschiedenen. Desweiteren wird eine Taste für Eïs und Fes (von C aus gesehen die übermäßige Terz oder die verminderte Quarte) sowie eine Taste für His (B♯) und Ces (von C aus gesehen die übermäßige Septime oder die verminderte Prime bzw. Oktave) eingeführt.
| Anzahl Tonschritte |
reelles Frequenzverhältnis |
genähertes rationales Frequenzverhältnis |
Name des Intervalls | Abweichung in Cent |
|---|---|---|---|---|
| 1 | 1.03201 | 31:30 | − 2.2 cent | |
| 2 | 1.06504 | 16:15 | kleine Sekunde (diatonischer Halbton) | − 2.6 cent |
| 3 | 1.09913 | 11:10 | undezimale neutrale Sekunde (größere Variante) | − 1.4 cent |
| 4 | 1.13431 | 8:7 | septimale große Sekunde | − 13.0 cent |
| 5 | 1.17062 | 7:6 | septimale kleine Terz | + 5.9 cent |
| 6 | 1.20809 | 6:5 | kleine Terz | + 11.6 cent |
| 7 | 1.24676 | 5:4 | große Terz | − 4.5 cent |
| 8 | 1.28666 | 9:7 | septimale große Terz | + 1.3 cent |
| 9 | 1.32785 | 4:3 | reine Quarte | − 7.1 cent |
| 10 | 1.37035 | 11:8 | undezimaler Tritonus | − 5.9 cent |
| 11 | 1.41421 | 17:12 | − 3.0 cent | |
| 12 | 1.45948 | 16:11 | Komplement des undezimalen Tritonus | + 5.9 cent |
| 13 | 1.50620 | 3:2 | reine Quinte | + 7.1 cent |
| 14 | 1.55441 | 14:9 | septimale kleine Sexte | − 1.3 cent |
| 15 | 1.60416 | 8:5 | kleine Sexte | + 4.5 cent |
| 16 | 1.65551 | 5:3 | große Sexte | − 11.6 cent |
| 17 | 1.70850 | 12:7 | septimale große Sexte | − 5.9 cent |
| 18 | 1.76318 | 7:4 | septimale kleine Septime (Naturseptime) | + 13.0 cent |
| 19 | 1.81962 | 11:6 | undezimale neutrale Septime (größere Variante) | − 13.0 cent |
| 20 | 1.87786 | 15:8 | große Septime | + 2.6 cent |
| 21 | 1.93797 | 29:15 | + 4.1 cent | |
| 22 | 2.00000 | 2:1 | Oktave | ± 0.0 cent |
Obwohl im gleichstufigen System mit 22 Tönen die große und kleine Terz mit ihren Frequenzverhältnissen von 5:4 und 6:5 enthalten sind, treten bei Abbildung der diatonischen Tonleiter auf das 22-stufige System – wie weiter unten beschrieben – aufgrund der sich daraus ergebenden Halb- und Ganztonabstände die septimalen Varianten der Terzen mit den Frequenzverhältnissen von 9:7 und 7:6 an ihre Stelle. Dort wo sich normalerweise die kleine Septime mit einem Frequenzverhältnis von 9:5 oder 16:9 findet, ist beim 22-stufigen System die konsonantere Naturseptime mit einem Frequenzverhältnis von 7:4 anzutreffen. Aufgrund des sehr oft auftretenden Faktors 7 in den Frequenzverhältnissen der Intervalle, sollten Musikinstrumente, die dieses Tonsystem verwenden, einen gut ausgeprägten 7. Oberton in ihrem Klang aufweisen.
In der indischen Musik wird laut Wikipedia die Oktave ebenfalls in 22 Schritte geteilt. Diese sind jedoch NICHT gleich groß!
Dieses Tonsystem entspricht dem 12-stufigen System bei dem jeder (Halb-)Tonschritt nocheinmal geteilt wird. Daher spricht man von "Viertelton-Musik".
| Anzahl (Viertel-)Tonschritte |
reelles Frequenzverhältnis |
genähertes rationales Frequenzverhältnis |
Name des Intervalls | Abweichung in Cent |
|---|---|---|---|---|
| 1 | 1.02930 | 33:32 | − 3.3 cent | |
| 2 | 1.05946 | 18:17 | + 1.0 cent | |
| 3 | 1.09051 | 12:11 | undezimale neutrale Sekunde (kleinere Variante) | − 0.6 cent |
| 4 | 1.12246 | 9:8 | große Sekunde (größere Variante) | − 3.9 cent |
| 5 | 1.15535 | 15:13 | + 2.3 cent | |
| 6 | 1.18921 | 6:5 | kleine Terz | − 15.6 cent |
| 7 | 1.22405 | 11:9 | undezimale neutrale Terz | + 2.6 cent |
| 8 | 1.25992 | 5:4 | große Terz | + 13.7 cent |
| 9 | 1.29684 | 13:10 | − 4.2 cent | |
| 10 | 1.33484 | 4:3 | reine Quarte | + 2.0 cent |
| 11 | 1.37395 | 11:8 | undezimaler Tritonus | − 1.3 cent |
| 12 | 1.41421 | 17:12 | − 3.0 cent | |
| 13 | 1.45565 | 16:11 | Komplement des undezimalen Tritonus | + 1.3 cent |
| 14 | 1.49831 | 3:2 | reine Quinte | − 2.0 cent |
| 15 | 1.54221 | 17:11 | − 3.6 cent | |
| 16 | 1.58740 | 8:5 | kleine Sexte | − 13.7 cent |
| 17 | 1.63392 | 13:8 | + 9.5 cent | |
| 18 | 1.68179 | 5:3 | große Sexte | + 15.6 cent |
| 19 | 1.73107 | 19:11 | + 3.8 cent | |
| 20 | 1.78180 | 16:9 | kleine Septime (kleinere Variante) | + 3.9 cent |
| 21 | 1.83401 | 11:6 | undezimale neutrale Septime (größere Variante) | + 0.6 cent |
| 22 | 1.88775 | 17:9 | − 1.0 cent | |
| 23 | 1.94306 | 33:17 | + 1.7 cent | |
| 24 | 2.00000 | 2:1 | Oktave | ± 0.0 cent |
Es ist zu erkennen, dass fünf der gegenüber dem 12-stufigen System hinzugewonnen Töne sehr exakt "undezimale" Intervalle darstellen, also Intervalle deren Frequenzverhältnisse als höchste Primzahl 11 aufweisen; so auch die undezimale neutrale Terz, die oft als Blue Note auftaucht. Leider sind in diesem Tonsystem die große und kleine Terz genauso schlecht getroffen, wie im 12-stufigen System.
| Anzahl Tonschritte |
reelles Frequenzverhältnis |
genähertes rationales Frequenzverhältnis |
Name des Intervalls | Abweichung in Cent |
|---|---|---|---|---|
| 1 | 1.02261 | 42:41 | − 3.0 cent | |
| 2 | 1.04573 | 22:21 | − 3.1 cent | |
| 3 | 1.06938 | 15:14 | septimaler diatonischer Halbton | − 3.3 cent |
| 4 | 1.09356 | 12:11 | undezimale neutrale Sekunde (kleinere Variante) | + 4.2 cent |
| 5 | 1.11829 | 9:8 | große Sekunde (größere Variante) | − 10.4 cent |
| 6 | 1.14357 | 8:7 | septimale große Sekunde | + 1.1 cent |
| 7 | 1.16943 | 7:6 | septimale kleine Terz | + 4.1 cent |
| 8 | 1.19587 | 6:5 | kleine Terz | − 6.0 cent |
| 9 | 1.22291 | 11:9 | undezimale neutrale Terz | + 1.0 cent |
| 10 | 1.25057 | 5:4 | große Terz | + 0.8 cent |
| 11 | 1.27884 | 9:7 | septimale große Terz | − 9.3 cent |
| 12 | 1.30776 | 17:13 | + 0.1 cent | |
| 13 | 1.33733 | 4:3 | reine Quarte | + 5.2 cent |
| 14 | 1.36757 | 11:8 | undezimaler Tritonus | − 9.4 cent |
| 15 | 1.39849 | 7:5 | Huygens' Tritonus (übermäßige Quarte) | − 1.9 cent |
| 16 | 1.43011 | 10:7 | Komplement von Huygens' Tritonus (verminderte Quinte) | + 1.9 cent |
| 17 | 1.46245 | 19:13 | + 1.1 cent | |
| 18 | 1.49552 | 3:2 | reine Quinte | − 5.2 cent |
| 19 | 1.52933 | 23:15 | − 4.5 cent | |
| 20 | 1.56391 | 11:7 | undezimale kleine Sexte | − 8.3 cent |
| 21 | 1.59928 | 8:5 | kleine Sexte | − 0.8 cent |
| 22 | 1.63544 | 18:11 | undezimale neutrale Sexte | − 1.0 cent |
| 23 | 1.67242 | 5:3 | große Sexte | + 6.0 cent |
| 24 | 1.71023 | 12:7 | septimale große Sexte | − 4.1 cent |
| 25 | 1.74890 | 7:4 | septimale kleine Septime (Naturseptime) | − 1.1 cent |
| 26 | 1.78845 | 9:5 | kleine Septime (größere Variante) | − 11.1 cent |
| 27 | 1.82889 | 11:6 | undezimale neutrale Septime (größere Variante) | − 4.2 cent |
| 28 | 1.87024 | 15:8 | große Septime | − 4.4 cent |
| 29 | 1.91253 | 21:11 | + 3.1 cent | |
| 30 | 1.95578 | 41:21 | + 3.0 cent | |
| 31 | 2.00000 | 2:1 | Oktave | ± 0.0 cent |
Obwohl dieses Tonsystem einige dissonante Intervalle enthält, so ist doch eine erstaunlich große Anzahl von konsonanten Intervallen mit sehr guter Genauigkeit getroffen. Insbesondere die auch im 12-stufigen System wichtigen Terzen sind hier mit nur 0.8 cent Abweichung bei der großen und mit nur 6.0 cent Abweichung bei der kleinen Terz vertreten. Quinte und Quarte haben mit 5.2 cent Abweichung zwar einen größeren Fehler als beim 12-stufigen System, dennoch ist diese Abweichung gemessen am Unterscheidungsvermögen des Menschen recht klein. Es finden sich noch eine Reihe von weiteren interessanten und nahezu exakt getroffenen Intervallen, so z.B. die undezimale neutrale Terz (Blue Note), Huygens' Tritonus mit einem Frequenzverhältnis von 7:5 oder die Naturseptime mit einem Frequenzverhältnis von 7:4.
Die Webseiten der Huygens-Fokker Foundation enthalten weiterführende Informationen zu Musik mit 31 gleichabständigen Tönen je Oktave.
Zu Anschauungszwecken habe ich folgendes Tastaturlayout entworfen:
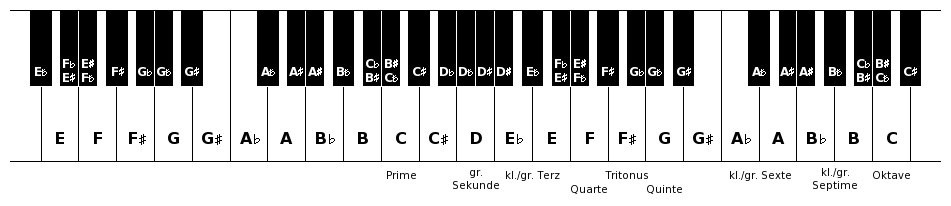
Die weißen Tasten entsprechen den Tönen, die man in der Notenschrift mit bis zu drei Vorzeichen (♭♭♭ bis ♯♯♯) ohne weitere Versetzungszeichen erreichen kann. Sie decken demnach die Töne folgender Tonleitern ab:
| Dur | E♭ | B♭ (b) | F | C | G | D | A |
|---|---|---|---|---|---|---|---|
| Moll (rein) | C | G | D | A | E | B (H) | F♯ |
| Moll (harmonisch) | C | G | D | A | – | – | – |
| Moll (melodisch) | C | G | D | A | – | – | – |
Diatonische Tonleitern umfassen 5 "Ganztonschritte" (A→B, C→D, D→E, F→G, G→A) sowie 2 "Halbtonschritte" (B/H→C, E→F). Möchte man eine Entsprechung zwischen einem gleichstufigen Tonsystem und der diatonischen Tonleiter bzw. dem Tonbezeichnungssystem mit den Tönen (C, C♯, D♭, D, usw.) finden, so muss die Gesamtschrittanzahl pro Oktave (z.B. 26) in fünf Ganztonschritte (z.B. 5 × 4) und zwei Halbtonschritte (z.B. 2 × 3) zerlegt werden (5 × 4 + 2 × 3 = 26).
Eine solche Zerlegung ist rein rechnerisch für folgende Anzahlen von Tonschritten pro Oktave möglich (Folge A162918 in OEIS):
12, 17, 19, 22, 24, 26, 27, 29, 31, 32, 33, 34, 36 bis 46, (47), 48, 49, 50, 51, (52), 53, (54), 55, 56, (57), 58, (59), 60, ...
In Klammern geschriebene Schrittanzahlen pro Oktave haben keine eindeutige Zerlegung.
Zur Beurteilung der Sinnhaftigkeit dieser Zerlegung in Halb- und Ganztonschritte, kann man die maximale Abweichung in Cent berechnen, die sich für einen Dur- oder Moll-Akkord im diatonischen System (z.B. die Töne C, E und G) gegenüber den reinen Verhältnissen ergibt. Die reinen Verhältnisse der kleinen und großen Terz sowie der Quinte sind 6:5, 5:4 und 3:2. Die beiden unterschiedlich großen Terzen ergeben die Quinte, da 6:5 × 5:4 = 3:2. Alternativ lassen sich jedoch auch die septimale kleine Terz mit dem Frequenzverhältnis von 7:6 und die septimale große Terz mit dem Frequenzverhältnis von 9:7 verwenden. Diese klingen zwar etwas dissonanter, ergeben jedoch ebenfalls gemeinsam die Quinte, da 9:7 × 7:6 = 3:2.
Für die interessantesten gleichstufigen Tonsysteme habe ich eine solche Berechnung vorgenommen:
| Gesamtanzahl Tonschritte pro Oktave |
Schrittanzahl enharmonisches Komma (z.B. C♯→D♭) |
Schrittanzahl chromatischer Halbton (z.B. D→D♯) |
Schrittanzahl diatonischer Halbton (z.B E→F) |
Schrittanzahl diatonischer Ganzton (z.B. F→G) |
maximaler Fehler der bei Dur- und Moll-Akkorden beteiligten Intervalle |
maximaler Fehler der bei Dur- und Moll-Akkorden beteiligten Intervalle in Bezug auf septimale Terzen |
|---|---|---|---|---|---|---|
| 12 | 0 | 1 | 1 | 2 | ±15.6 cent | ±35.1 cent |
| 17 | −1 | 2 | 1 | 3 | ±37.2 cent | ±15.5 cent |
| 19 | 1 | 1 | 2 | 3 | ±7.4 cent | ±56.1 cent |
| 22 | −2 | 3 | 1 | 4 | ±50.0 cent | ±7.1 cent |
| 24 | 0 | 2 | 2 | 4 | ±15.6 cent | ±35.1 cent |
| 26 | 2 | 1 | 3 | 4 | ±17.1 cent | ±65.9 cent |
| 27 | −3 | 4 | 1 | 5 | ±58.1 cent | ±9.4 cent |
| 29 | −1 | 3 | 2 | 5 | ±27.5 cent | ±22.8 cent |
| 31 | 1 | 2 | 3 | 5 | ±6.0 cent | ±48.0 cent |
| 34 | −2 | 4 | 2 | 6 | ±37.2 cent | ±15.5 cent |
| 41 | −1 | 4 | 3 | 7 | ±23.4 cent | ±25.8 cent |
| 46 | −2 | 5 | 3 | 8 | ±31.1 cent | ±20.1 cent |
| 53 | −1 | 5 | 4 | 9 | ±21.3 cent | ±27.5 cent |
Sinnvoll in das diatonische System einzuordnen sind gleichstufige Tonsysteme mit folgender Anzahl von Tönen pro Oktave: 12, 17, 19, 22, 24, 26, 27, 31 sowie 34, wobei die Anzahlen 17, 22, 27 und 34 zu einer Verwendung der septimalen Varianten der Terzen führen. Bei Verwendung von normalen (nicht septimalen) Terzen schneidet das System mit 31 Tonschritten je Oktave am besten ab. Es eignet sich ausserdem hervorragend zu Anschauungszwecken, da das enharmonische Komma, der chromatische Halbton, der diatonische Halbton sowie der diatonische Ganzton alle unterschiedlich groß sind und das enharmonische Komma positiv ist (D♭ ist höher als C♯). Möchte man septimale Terzen verwenden, dann ist das 22-stufige System die beste Wahl.
Folgende Animation zeigt mögliche Anordnungen vom 12- bis zum 26-stufigen System auf einer (hypothetischen) Universalklaviatur:
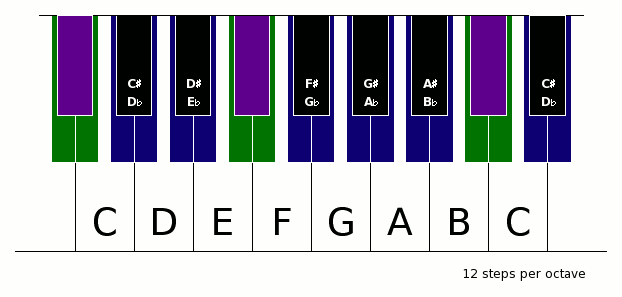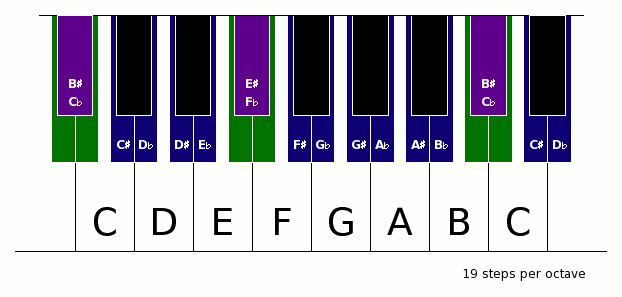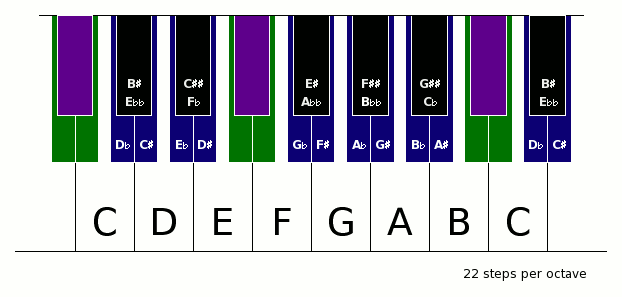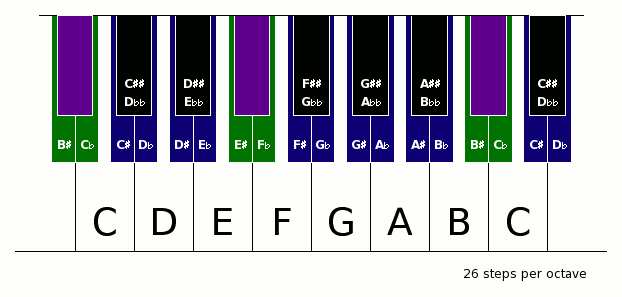
Aufgrund der oben erwähnten interessanten Eigenschaften des 31-stufigen Systemes und der praktischen Verbreitung des 12-stufigen Systemes sind im Folgenden die Abweichungen in Cent der wichtigen Töne beider Systeme angegeben. Um die Abweichungen insgesamt so klein wie möglich zu halten, wurde der Ton D beider Systeme aufeinander abgestimmt.
| 12-stufig | 31-stufig | Differenz | |
|---|---|---|---|
| C | 0 cent | 6.5 cent | +6.5 cent |
| C♯ | 100 cent | 83.9 cent | −16.1 cent |
| D♭ | 100 cent | 122.6 cent | +22.6 cent |
| D | 200 cent | 200.0 cent | ±0.0 cent |
| D♯ | 300 cent | 277.4 cent | −22.6 cent |
| E♭ | 300 cent | 316.1 cent | +16.1 cent |
| E | 400 cent | 393.5 cent | −6.5 cent |
| F | 500 cent | 509.7 cent | +9.7 cent |
| F♯ | 600 cent | 587.1 cent | −12.9 cent |
| G♭ | 600 cent | 625.8 cent | +25.8 cent |
| G | 700 cent | 703.2 cent | +3.2 cent |
| G♯ | 800 cent | 780.6 cent | −19.4 cent |
| A♭ | 800 cent | 819.4 cent | +19.4 cent |
| A | 900 cent | 896.8 cent | −3.2 cent |
| A♯ | 1000 cent | 974.2 cent | −25.8 cent |
| B♭ (b) | 1000 cent | 1012.9 cent | +12.9 cent |
| B (H) | 1100 cent | 1090.3 cent | −9.7 cent |
| C | 1200 cent | 1206.5 cent | +6.5 cent |
Die 7 Grundtöne der C-Dur- oder der reinen A-Moll-Tonleiter, die entsprechend den weißen Tasten einer normalen Klaviertastatur auf weißem Hintergrund dargestellt sind, haben alle eine Abweichung von weniger als 10 cent, und somit die geringsten Abweichungen voneinander. Die weiteren Töne, die sich in der Notenschrift mit bis zu drei Vorzeichen (♭♭♭ bis ♯♯♯) darstellen lassen sind hier grau hinterlegt und weisen alle eine Abweichung von weniger als 20 cent auf.
Urheber des Textes und aller Bilder: Jan Behrens (2008-2009)
Es wird unentgeltlich jeder Person das Recht eingeräumt, Kopien dieses Dokumentes zu benutzen, zu kopieren, zu modifizieren, mit anderen Werken zu kombinieren, zu veröffentlichen, zu verbreiten, unterzulizensieren, zu verkaufen und/oder weiteren Personen diese Rechte einzuräumen, soweit in allen Kopien oder wesentlichen Teilen davon der Autor genannt wird und dieser Hinweistext enthalten bleibt. Fehlerfreiheit und Eignung für einen bestimmten Zweck werden nicht zugesichert; Verwendung erfolgt auf eigenes Risiko. Bei einer Verwendung für Bildungszwecke darf auf die Nennung des Autors und das Anfügen dieses Hinweises verzichtet werden. Dieser Absatz gilt NICHT für die Hörbeispiele, auf die in diesem Dokument verwiesen wird, da diese im Internet gefundene veröffentlichte Werke Dritter sind, deren Urheberrechte gesondert beachtet werden müssen!
Zurück zur Hauptseite